Combinational Circuits

Amu_Ke_Fundye

Combinational Circuits

Logic Circuits can be divided into two types.

• Combinational Logic Circuit, and
• Sequential Logic Circuit.

Combinational Logic Circuit:

A combinational logic circuit consists of logic gates whose output is determined by the combination of current inputs.

• It consists of input variables, logic gate and output variables.
• No feedback is required.
• No memory is required.

• Examples of Combinational Circuits: Multiplexer, Decoder, Encoder, Parallel Adders, etc.

Sequential Logic Circuit:

This Circuit consists of logic gates arranged in parallel and its output is determined by the combination of the current input and the prior output. Sequential circuit also contains memory elements that are capable to store the information of the prior output.

• Examples of Sequential Circuits: Flip-flops, Shift Registers, Counters, etc.

Logic Gates

A logic gate is an idealised or physical device implementing a Boolean function, that is, it performs a logical operation in one or more logical inputs and produces a single logical output.

The logic gates can be classified as

• NOT, AND, OR, are basic gates.
• NAND, NOR are universal gates.
• EXOR, EXNOR are arithmetic circuit or code convertor or comparators.

NOT Gate (Inverter)

Truth Table

AND Gate

Properties of AND logic:

1. Commutative Law: AB = BA
2. Associative Law: ABC = (AB) C = (AC)B = A(BC)

OR Gate Truth Table

Properties of OR logic:

1. Commutative Law: A + B = B + A
2. Associative Law: (A + B + C) = (A + B) + C = A + (B+ C)

NAND Gate

Properties of NAND logic:

1. Commutative Law: 
2. Associative Law: 

NOR Gate

• NOR gate follows commutative law but not follow associative law

EXOR Gate

Properties of EXOR Logic:

• Enable input = 0
• Disable input = 1
• It is also called stair case switch.
• It is widely used in parity generation and detection.
• When both the inputs are different, then output becomes high or logic 1.
• When both the inputs are same, then output becomes low or logic 0.

Note: 

EXNOR Gate

Properties of EXNOR Gate:

• Enable input = 1
• Disable input = 0
• When both the inputs are same, then output .becomes high or logic 1.
• When both the inputs are different, then output becomes low or logic 0.

Logic Gate Conversions

• OR Gate using NAND Gate:

• AND Gate using NOR Gate:

• NAND Gate using NOR Gate

• NOR Gate using AND Gate

NAND and NOR Gate as Universal Gate

NAND Gate as Universal Gate

Boolean Algebra

1. NOT-Operation theorem: 
2. AND-Operation theorem: 
3. OR-Operation theorem: 
4. Distribution theorem: A + BC = A (A + B)(A + C)
   Note: 
5. Demorgan’s Theorem: 
6. Transposition Theorem: (A + B) (A + C) = A + BC
7. Consensus Theorem: This theorem is used to eliminate redundant term. It is applicable only when if a boolean function contains three variables. Each variable used two times. Only one variable is complemented or uncomplemented. Then the related terms so that complemented or uncomplemented variable is the answer. 

SOP (Sum of Product): (Minimum Term)

A sum of product expression is two or more AND functions or functions together. Each product term is known as minimum term.

• SOP expression is used when output becomes logic 1.
• Example: 
  • three minterms are there in the expression

POS (Product of Sum): (Maximum Term)

It is the AND function of two or more OR function each sum term is known as maximum term.

• POS expression is used when output is logic ‘0’.
• Example:
  • Three max terms are there in the expression

Note:

With’ n’ variables maximum possible minimum and maximum terms = 2ⁿ

With’ n’ variables maximum possible logic expression = 

Duality Theorem: To convert positive logic into negative logic and vice-versa, dual function are used.

• Change each AND sign by OR sign and vice versa (↔ +)
• Complement any 0 or l appearing in expression.
• Keep variable as it is.
• Example: 

Representation of K-map: With n-variable Karnaugh-map, there are 2ⁿ cells.

Example:

• 2 –variable K Map:

• 3 –variable K Map:

• 4 –variable K Map:

Designing Combinational Circuits: The steps to design combinational circuits are as the following:

1. Understand the problem
2. Find the required number of input and output variables
3. Construct a truth table using the relationship between the input and output
4. Obtain the Boolean function or the logical expression from the truth table using Karnaugh Map.
5. Draw a logic circuit based on the obtained logical expression.

Arithmetic Circuits

Arithmetic circuits are used to perform addition and subtraction. Binary adder performs binary addition and binary subtractor performs binary subtraction.

Classification of Adder: (i) Half Adder and (ii) Full Adder

Classification of Subtractor: (i) Half Subtractor and (ii) Full Subtractor

Half Adder: This circuit is used for addition of two one bit numbers.

• Truth table of Half Adder:

• Half adder circuit:

Sum (S) = 

Carry (C) = AB

• Implement of Half Adder Using NAND Gate:

Note: Required number of NAND Gates to implement Half Adder = 5

• Implement of Half Adder Using NOR Gate:

Note: Required number of NOR Gates to implement Half Adder = 5

Full Adder

A full adder is a combinational logic circuit that performs the arithmetic sum of three input bits. It consists of three inputs and two outputs.

Truth table for Full Adder:

Logic diagram of Full Adder:

• Sum (S) = 
• Carry (C₀) = AB + BC + AC

• A full adder = 2 Half adder + 1 OR Gate
• Required minimum number of NAND gate to implement FA = 9
• Required minimum number of NOR gate to implement FA = 9

Half Subtractor

It is a combinational logic circuit that subtracts two bit and produces their difference and borrow.

Logic Diagram of Half Subtractor:

• Difference (D) 
• Borrow (B₀) = 
• To implement half subtractor the total number of NAND/NOR are required = 5

Full Subtractor

It is a combinational logic circuit that performs subtraction involving three bit namely minued bit, subtrahend bit and borrow from the previous stage

• Difference (D) 
• 
• A full subtractor = 2 half subtractor + 1 OR gate
• To implement full subtractor of NAND/NOR gates are required = 9

Multiplexer (MUX)

• It is a combinational circuit that selects binary information from one of the many input lines and directs it to a single output line.
• The selection of a particular input line is controlled by a set of selection lines.
• MUX is also called: Many to one, Data selector, Universal circuit, or Parallel data serial.
• Multiplexing means transmitting a large number of information units over a smaller number of channels or lines. It is abbreviated as MUX.
• There are 2ⁿ input lines and n selection lines whose bit combinations determine which input is selected.

m = 2ⁿ implies n = log m where m = Number of data inputs, and n = Number of select lines.

2 × 1 MUX:

Universal equation 

Implementation of one MUX using another MUX:

Demultiplexer (DEMUX)

• It is a circuit that receives information on a single line and transmits this information on one of 2ⁿ possible output lines.
• The selection of a specific output line is controlled by the bit values of n selected lines.

1 × 2 Demux:

D₀ = S′I

D₁ = SI

• Truth table of 1 × 2 Demux:

• Circuit Diagram of 1 × 2 Demux:

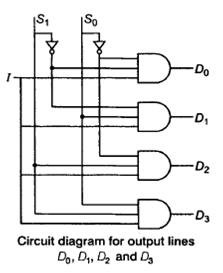
• 1 × 4 Demux:
  • 
  • 
  • 
  • 

• Truth table of 1 × 4 Demux:

• Circuit Diagram of 1 × 4 Demux:

• DEMUX Implementation using another DEMUX:

Decoders

• A decoder is a combinational circuit that converts binary information from n input lines to a maximum 2ⁿ unique output lines.
• If the n-bit decoded information has unused or don’t-care combinations, the decoder output will have fewer than 2ⁿ outputs.
• The decoders presented here are n-to-m-line decoders, where m ≤ 2ⁿ. Their purpose is to generate the 2ⁿ (or fewer) minterms of n input variables.

2 × 4 Decoder:

• 
• 
• 
• 

Tutht table of 2 × 4 Decoder:

Encoders

• It is a combinational circuit that converts information into coded form (binary).
• It is a digital circuit that performs the inverse operation of a decoder.
• An encoder has 2ⁿ (or fewer) input lines and n output lines.
• The output lines generate the binary code corresponding to the input value.

Regards 

Amrut Jagdish Gupta